⭐ DeepSeek-R1 Was Only The Beginning

Test-Time Scaling and Reinforcement Learning's success continues

Feb 14, 2025

1B model > 405B model
AI winning Olympic Gold
Generating world models on the fly

1. Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling

Watching: Compute-Optimal TTS (paper/code soon™)

What problem does it solve? The article addresses the challenge of optimizing Test-Time Scaling (TTS) for Large Language Models (LLMs) – the practice of using extra computation during inference to boost performance. Current methods lack systematic analysis of how factors like policy models (LLMs generating solutions), reward models (PRMs guiding solution quality), and problem difficulty influence TTS efficiency, limiting practical adoption. The work questions whether small LLMs (e.g., 1B parameters) can surpass massive ones (e.g., 405B) via optimized TTS strategies.

How does it solve the problem? The authors conducted extensive experiments on mathematical reasoning tasks (MATH-500, AIME24) using diverse policy models (0.5B to 72B), Process Reward Models (PRMs), and TTS methods like beam search. They introduced a reward-aware compute-optimal TTS strategy that adapts computation based on task complexity, model capability, and PRM feedback. Absolute problem difficulty thresholds (e.g., "hard" = 0-10% baseline accuracy) replaced percentile-based groupings for better alignment.

What are the key findings? Smaller models, when paired with tailored TTS strategies, surpassed much larger counterparts: a 1B model outperformed a 405B model on MATH-500, and a 7B model exceeded GPT-4o and DeepSeek-R1 on AIME24—with higher inference efficiency. Performance gains depended critically on aligning PRMs to policy models (e.g., PRMs trained on aligned data improved search efficiency by 2x) and scaling compute budgets inversely with model size (smaller models benefited more from increased sampling).

Why does it matter? It shows that strategic runtime computation allocation can beat raw model size, enabling cheaper, environmentally-friendly models to match or exceed trillion-parameter behemoths. For real-world deployments—where serving costs dominate R&D expenses—this opens paths to replace expensive, energy-hungry models with resource-efficient ones. The results also suggest that PRMs trained on small models could guide even weaker LLMs to solve problems only solvable by much larger models today, potentially democratizing high-performance reasoning.

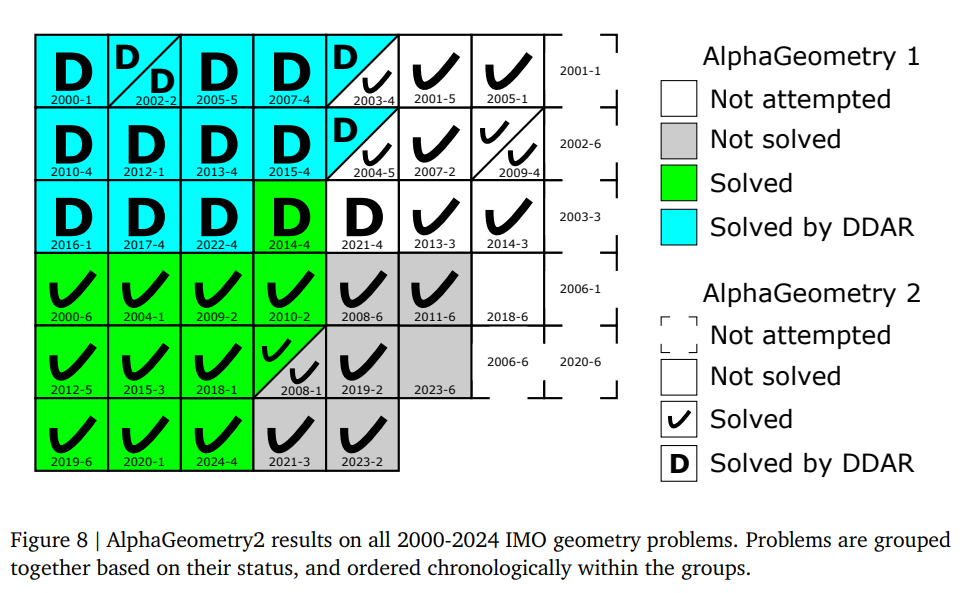
2. Gold-medalist Performance in Solving Olympiad Geometry with AlphaGeometry2

Watching: AlphaGeometry2 (paper)

What problem does it solve? AlphaGeometry2 addresses the challenge of getting AI systems to solve advanced math competition problems at gold-medalist human levels. While earlier systems like AlphaGeometry (AG1) could solve basic Olympiad geometry questions, they struggled with "creative" challenges involving moving points (e.g., tracing a circle’s path), non-constructive definitions (e.g., "find all points X where angle ABX = 30°"), and complex algebraic relations. These gaps limited AG1 to solving just 54% of IMO-level problems – falling short of top human performance.

How does it solve the problem? The team upgraded AlphaGeometry in four key areas. First, they expanded its "math vocabulary" to describe problems like those involving ratios, angles, and dynamic scenarios (e.g., moving points). Second, they turbocharged its logical reasoning engine to run 300 times faster, letting it explore more solutions. Third, they trained new models using Google’s Gemini architecture to better predict helpful geometric constructions (like adding imaginary lines). Finally, they designed a clever search system where multiple AI "thinkers" share ideas mid-solve – one focuses on depth-first exploration, another on breadth-first, and they swap useful clues.

What are the key findings? AlphaGeometry2 achieved an 84% solve rate on 2000-2024 IMO geometry problems – surpassing the average gold medalist (61%). Its expanded language now covers 88% of IMO problems (vs 66% before), and it solves tougher "shortlist" problems human experts consider unsolvable without advanced techniques like inversion. Notably, the system solved problems like IMO 2024’s P4 with creative, non-human strategies – like introducing an obscure auxiliary point to unlock angle relationships – suggesting AI can pioneer new proof techniques.

Why does it matter? This work bridges two AI paradigms: neural networks (good at intuition/creativity) and symbolic systems (reliable at step-by-step logic). It shows how combining them can crack structured STEM problems requiring both "aha!" insights and rigor – a blueprint for future tools in math, physics, or code verification. Practically, systems like AlphaGeometry2 could democratize advanced math coaching and inspire AI collaborators for theorem discovery. The automated translation of word problems into formal code also hints at broader applications, like parsing textbook questions into executable simulations.

3. Generating Symbolic World Models via Test-time Scaling of Large Language Models

Watching: Symbolic World Models (paper)

What problem does it solve? Large Language Models (LLMs) struggle with complex planning tasks that require precise logical reasoning, like managing constraints (e.g., robot movement rules) or tracking state transitions (e.g., block positions). The issue stems from natural language's ambiguity, which makes it hard to represent states clearly. For example, if an LLM generates "move block A," it might not fully grasp dependencies like Block B must support A. This ambiguity can lead to impossible or unsafe plans. The paper addresses this by using PDDL, a programming-like language, to formalize states and actions explicitly.

How does it solve the problem? They turned LLMs into "PDDL translators": first, they used Best-of-N sampling to generate multiple draft PDDL code snippets (like asking the model to brainstorm 8 versions). Then, they refined the best draft using iterative Verbalized Machine Learning (iVML)—a feedback loop where one LLM critiques logical errors in the code (e.g., "Stacking blocks without checking if the base is clear") and another LLM updates it. Importantly, this doesn’t require training data; the system improves through prompts alone. For example, if a PDDL action misses a precondition, iVML flags it like a teacher correcting code syntax.

What are the key findings? The hybrid approach (BoN + iVML) achieved 85.2% success in translating natural language to PDDL domains, outperforming even OpenAI’s specialized models (o1-mini scored 41.7%). When combined with classic planners like A*, the generated PDDL models solved notoriously hard tasks (e.g., robot block-stacking in Termes), where direct LLM planning failed completely. Code-specialized LLMs (Qwen-Coder) worked best, as their code-like training aligned with PDDL’s structure.

Why does it matter? This bridges the gap between LLMs’ fuzzy reasoning and rigorous planning demands in robotics, logistics, or industrial automation. By translating natural language to PDDL, LLMs can "hand off" complex state management to optimized algorithms (like A*), avoiding hallucinations. This hybrid approach unlocks real-world use cases where safety-critical systems require provably correct plans (e.g., ensuring a robot never drops a block mid-air). It also reduces reliance on scarce PDDL experts—automating what used to take hours of manual coding.

LLM Watch

Discussion about this post