🧠 How LLMs Actually "Think" and Memorize

Learn about LLM Compression, AlphaOne and the 3.6 bits-barrier

Welcome, Watcher! This week in LLM Watch:

1. How well do LLMs compress meaning?

2. Machines Thinking Slow, Thinking Fast

3. How and when LLMs actually generalize

Don’t forget to subscribe to never miss an update again.

---

1. From Tokens to Thoughts: How LLMs and Humans Trade Compression for Meaning

Watching: Compression vs. Meaning (paper)

What problem does it solve? Understanding how Large Language Models (LLMs) represent knowledge is crucial for advancing AI, yet we don't fully grasp whether they process concepts like humans do. While humans excel at semantic compression - organizing diverse instances into meaningful categories (like grouping robins and eagles as "birds") - this process involves a delicate balance. We trade off between keeping representations simple and preserving semantic richness. The fundamental question is: Do LLMs achieve this same balance between compression and meaning that characterizes human cognition, or do they use fundamentally different strategies?

How does it solve the problem? The researchers (among them, Yann LeCun) developed a new information-theoretic framework combining Rate-Distortion Theory and the Information Bottleneck principle to quantitatively measure how both humans and LLMs balance compression with semantic fidelity. They analyzed token embeddings from various LLMs (ranging from BERT to Llama models) and compared them against classic human categorization benchmarks from cognitive psychology. Using metrics like mutual information and clustering analysis, they assessed conceptual alignment, internal semantic structure, and overall representational efficiency between human and AI systems.

What are the key findings? The study reveals a fundamental divergence in how LLMs and humans manage information. While LLMs successfully form broad categories that align with human judgment, they fail to capture fine-grained semantic distinctions like item typicality (e.g., recognizing that a robin is a more "typical" bird than a penguin). Most strikingly, LLMs demonstrate aggressive statistical compression - they minimize redundancy and maximize efficiency by information-theoretic measures. In contrast, human conceptual systems appear "inefficient" by these metrics, suggesting humans optimize for adaptive richness and contextual flexibility rather than pure compression.

Why does it matter? These results challenge the assumption that scaling up LLMs will naturally lead to human-like understanding. The stark difference in representational strategies suggests that current AI architectures may be fundamentally limited in achieving genuine comprehension. While LLMs excel at statistical pattern matching through aggressive compression, human cognition prioritizes semantic richness and adaptive flexibility - qualities essential for navigating complex, real-world scenarios. This might be crucial for developing next-generation AI systems that move beyond surface-level mimicry toward deeper, more human-aligned understanding.

---

---

2. AlphaOne: Reasoning Models Thinking Slow and Fast at Test Time

Watching: AlphaOne (paper/code coming soon)

What problem does it solve? Large Reasoning Models (LRMs) like OpenAI's o1 and DeepSeek-R1 have shown remarkable abilities in complex reasoning tasks, but they suffer from a Goldilocks problem - they either think too much (overthinking) or too little (underthinking). Think of it like a student solving a math problem who either gets stuck in unnecessary calculations or rushes through without proper consideration. These models struggle to find the sweet spot between what psychologists call System 1 (fast, intuitive thinking) and System 2 (slow, deliberate thinking). Current approaches try to fix this by either forcing more thinking or cutting it short, but these one-size-fits-all solutions aren't optimal for different types of problems.

How does it solve the problem? AlphaOne (α1) acts like a smart reasoning scheduler. The key innovation is the "α moment" - imagine it as a timer that determines how long the model should spend in its thinking phase, scaled by a parameter α. Before this moment, α1 uses a clever probability-based system (Bernoulli process) to insert "wait" tokens that trigger slower, more careful thinking - like adding strategic pauses in a conversation. After the α moment, it switches gears by replacing any further "wait" tokens with end-of-thinking markers, essentially telling the model "okay, time to wrap up and give your answer." This creates a natural slow-to-fast reasoning flow, rather than the rigid all-or-nothing approaches used before.

What are the key findings? The empirical results across mathematical, coding, and scientific benchmarks show that α1 significantly outperforms existing methods in both reasoning quality and efficiency. The framework demonstrates superior performance while being more flexible than previous approaches - it can handle both sparse adjustments (occasional tweaks) and dense modulation (frequent fine-tuning) of the reasoning process. Importantly, α1 successfully balances the trade-off between thinking deeply enough to solve complex problems and being efficient enough to be practical, achieving what the authors call "dense slow-to-fast reasoning modulation."

Why does it matter? These findings matter because they provide a practical solution to make AI reasoning both smarter and more efficient. As LLMs are increasingly deployed for complex tasks in science, mathematics, and programming, having a framework that can dynamically adjust reasoning depth based on the problem at hand is crucial. α1's approach is particularly valuable because it's universal - it can be applied to different models and doesn't require retraining. This means existing LRMs can be immediately improved, making them more reliable for real-world applications where both accuracy and computational efficiency matter. The work also provides insights into how AI reasoning differs from human cognition, suggesting that optimal AI reasoning might follow different patterns than human thought processes.

---

3. How much do language models memorize?

Watching: LLM Memorization (paper)

What problem does it solve? The widespread deployment of large language models has raised critical questions about what these models actually memorize from their training data. While previous work has tried to measure memorization through extraction attacks or membership inference, these approaches fail to distinguish between genuine memorization and generalization. For instance, if a model correctly answers "What is 2^100?", is it memorizing the specific answer or generalizing from mathematical patterns? This distinction matters enormously for understanding model capacity, privacy risks, and the fundamental nature of how LLMs store and retrieve information.

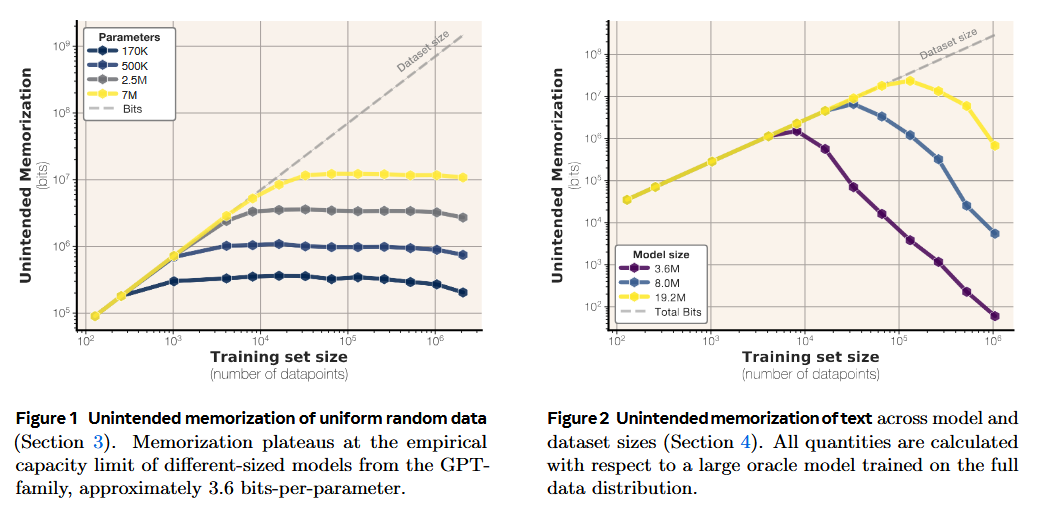
How does it solve the problem? The authors propose a new framework that decomposes memorization into two distinct components: unintended memorization (information about specific datasets) and generalization (knowledge about the underlying data-generation process). They leverage compression theory and Kolmogorov complexity to quantify memorization in bits. To isolate pure memorization from generalization, they first train models on uniformly random bitstrings where no generalization is possible. Then they repeat experiments with real text, using larger "oracle" models as references to separate sample-specific memorization from general patterns. This clever approach allows them to measure the exact information capacity of transformer models.

What are the key findings? They discovered that GPT-style transformers have a remarkably consistent capacity of approximately 3.6 bits-per-parameter, regardless of model size. They observed that models memorize training data until reaching this capacity limit, at which point "grokking" occurs - the model shifts from memorizing individual samples to learning generalizable patterns. This transition point coincides exactly with the double descent phenomenon. Additionally, they developed scaling laws that accurately predict membership inference performance based on model capacity and dataset size, showing that modern LLMs trained on massive datasets make reliable membership inference practically impossible for average datapoints.

Why does it matter? These results provide the first principled measurement of language model capacity and offer a unified explanation for several puzzling phenomena in deep learning. The 3.6 bits-per-parameter finding gives us a concrete limit on how much information models can store, crucial for understanding privacy risks and designing training datasets. The connection between capacity, memorization, and double descent provides theoretical grounding for empirical observations that have long puzzled researchers. Perhaps most practically, the scaling laws for membership inference suggest that current large-scale training practices naturally provide some privacy protection simply through scale - a finding with significant implications for both model developers concerned about data leakage and researchers studying model behavior.

---

---

Papers of the Week:

1. ProRL: Prolonged Reinforcement Learning Expands Reasoning Boundaries in Large Language Models

2. Can Large Reasoning Models Self-Train?

3. Navigating the Latent Space Dynamics of Neural Models

4. REASONING GYM: Reasoning Environments for Reinforcement Learning with Verifiable Rewards

5. Beyond the 80/20 Rule: High-Entropy Minority Tokens Drive Effective Reinforcement Learning for LLM Reasoning

6. Darwin Godel Machine: Open-Ended Evolution of Self-Improving Agents

7. Seed-Coder: Let the Code Model Curate Data for Itself

8. VisCoder: Fine-Tuning LLMs for Executable Python Visualization Code Generation

9. RewardAnything: Generalizable Principle-Following Reward Models

---

👍 If you enjoyed this article, give it a like and share it with your peers.

---